this post was submitted on 16 Jun 2024
1185 points (97.8% liked)
Memes
54682 readers
2192 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 6 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
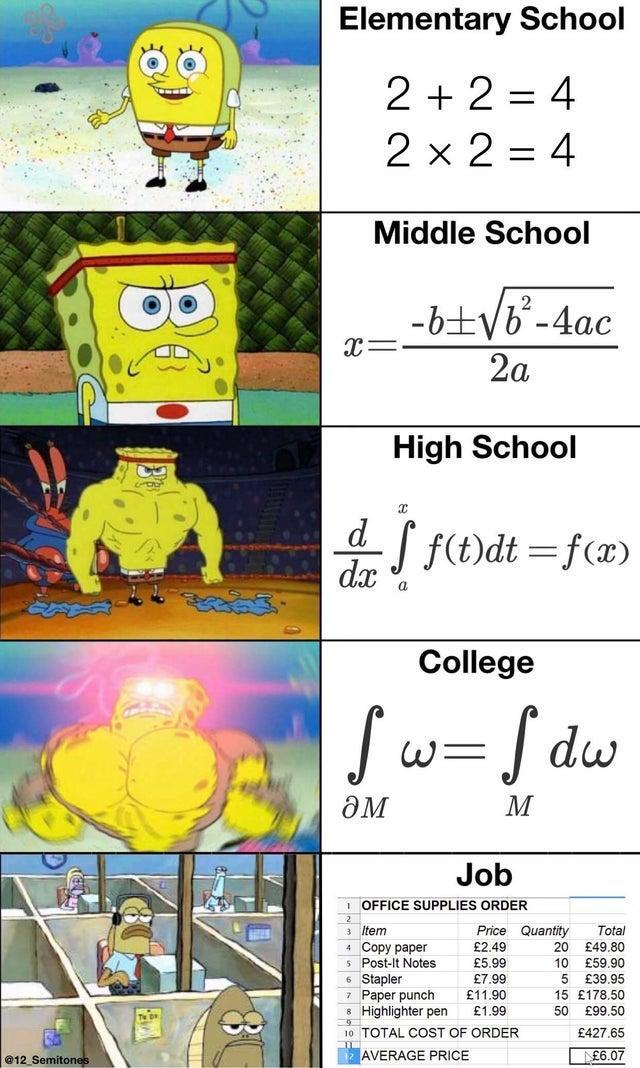
What's the college one mean?
Stokes' theorem. Almost the same thing as the high school one. It generalizes the fundamental theorem of calculus to arbitrary smooth manifolds. In the case that M is the interval [a, x] and ω is the differential 1-form f(t)dt on M, one has dω = f'(t)dt and ∂M is the oriented tuple {+x, -a}. Integrating f(t)dt over a finite set of oriented points is the same as evaluating at each point and summing, with negatively-oriented points getting a negative sign. Then Stokes' theorem as written says that f(x) - f(a) = integral from a to x of f'(t) dt.
It's the most general form of Stokes' theorem that the integral of a differential form over the boundary of an volume and the integral of an exterior derivative of this form over that volume are the same. It covers a lot of classic formulas from the fundamental theorem of calculus to Green's theorem, Gauss' theorem and classic Stokes' theorem.
Same as high school but fancier?