Sources are important not just for what they say but how they say it, where they say it, and why they say it.
None of which you've addressed since I gave you the source. Remember when you said this...
you can’t identify authors, you can’t check for bias
So, did you do that once I gave you the link? And/or are you maybe going to address "what they say but how they say it, where they say it, and why they say it" in regards to the link I gave you?
You keep reiterating your point as if it is established fact,
What they teach in Maths textbooks aren't facts? Do go on. 😂
tell me how it supports you
I did, and you've apparently refused to read the relevant part.
in comparison to a Phd
You know not all university lecturers do a Ph.D. right? In which case they haven't done any more study at all. But I know you really wanna hang on to this "appeal to authority" argument, since it's all you've got.
I have no interest in continuing this discussion
Yeah I saw that coming once I gave you the link to the textbook.
including the ‘highschool’ math
...when they were in high school.
teach the same (or similar) curriculum each and every year
There you go. Welcome to why high school teachers are the expert in this field.
math textbooks as the ultimate solution and so, so many of them are written by professors
So wait, NOW you're saying textbooks ARE valid in what they say? 😂
I want to point out that your only two sources
All that points out is that you didn't even read THIS thread properly, never mind the other one. Which two are they BTW? And I'll point out which ones you've missed.
I assume you accepted that seeing as you did not respond to that point
Well, I'll use your own logic then to take that as a concession, given how many of my points you didn't respond to (like the textbook that I gave you the link to, and the Cajori ab=(ab) one, etc.).
I’ve given 3 sources,
3 articles you mean.
all of which you dismiss simply because
...all of them have forgotten about The Distributive Law and Terms., which make the expression totally unambiguous. Perhaps you'd like to find an article that DOES talk about those and ALSO asserts that the expression is "ambiguous"? 😂 Spoiler alert: every article, as soon as I see the word "ambiguous" I search the text for "distributive" and "expand" and "terms" - can you guess what I find? 😂 Hint: Venn diagram with little or no overlap.
I could probably find some highschool textbooks that support weak juxtaposition if I searched,
Do you wanna bet on that? 😂
without ever providing a source that explains these rules
They're in my thread, if you'd bothered to read any further. By your own standards, 😂I'll take it that you concede all of my points that you haven't responded to.
I expect you to have a mathematical proof for why weak juxtaposition would never work, one that has no flaws. Otherwise, at best you have a hypothesis
You know some things are true by definition, right, and therefore don't have a proof? 1+1=2 is the classic example. Or do you challenge that too?
So do YOU have a hypothesis then? How "weak juxtaposition" could EVER work given "strong juxtaposition" is the only type ever used in any of the rules of Maths? I'll wait for your proof...


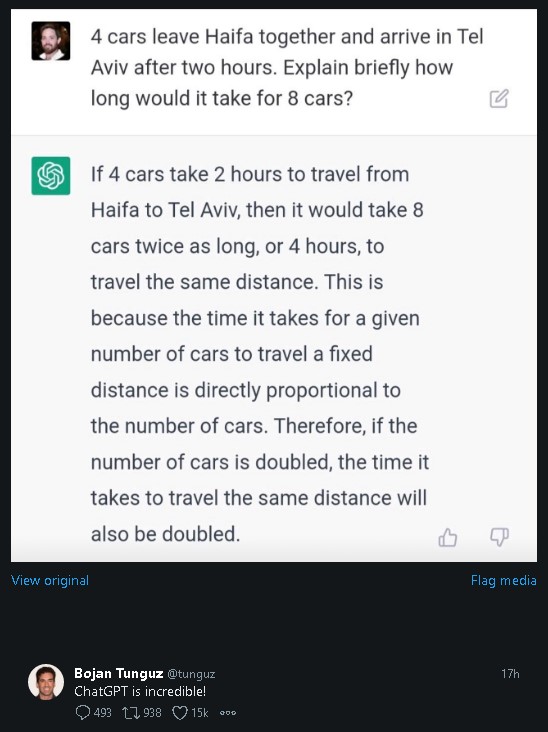
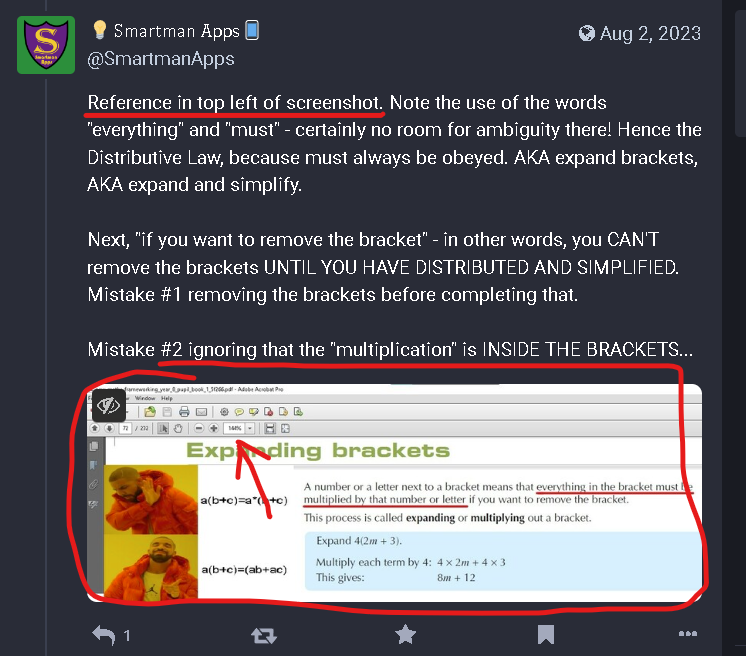
You know EXACTLY where I said those things, and you've been avoiding addressing them ever since because you know they prove the point that #MathsIsNeverAmbiguous See ya.