SmartmanApps

That'd be good, but what I've found so far here is a whole bunch of people who don't like being told the actual facts of the matter! 😂

only refers to implicit multiplication involving special expressions(?) like pi, e, sqrt or log, and nothing about “regular” implicit multiplication like 2(1+3)

That was a very astute observation you made there! The fact is, for the very reason you stated, there is in fact no such thing as "implicit multiplication" - it is a term which has been made up by people who have forgotten Terms (the first thing you mentioned) and The Distributive Law (the second thing you mentioned). As you've noted., these are 2 different rules, and lumping them together as one brings exactly the disastrous results you might expect from lumping different 2 rules together as one...

See here for explanation of all the various rules, including textbook references and proofs.

Read the damn article.

Read it. Was even worse than I was expecting! Did you not notice that a blog about the alleged ambiguity in order of operations actually disobeyed order of operations in a deliberately ambiguous example? I wrote 5 fact check posts about it starting here - you're welcome.

Let me know if you ever decide to read the article instead of arguing against an imagined opponent

Read it, wasn't imagined. In fact it was even worse than I thought it would be! Did you not notice about how a blog about the alleged ambiguity in order of operations actually disobeyed order of operations in a deliberately ambiguous example? I wrote 5 Fact check posts, starting here - you're welcome.

FACT CHECK 5/5

most people just dismiss that, because they “already know” the answer

Maths teachers already know how to do Maths. Huh, who would've thought? Next thing you'll be telling me is English teachers know the rules of grammar and how to spell!

and a two-sentence comment can’t convince them how and why it’s ambiguous

Literally NOTHING can convince a Maths teacher it's ambiguous - Maths teachers already know all the rules of Maths, and which ones you're breaking

Why read something if you have nothing to learn about the topic that’s so simple that you know for a fact that you are right

To fact check it for the benefit of others

At this point I hope you understand how and why the original problem is ambiguous

At this point I hope you understand why it isn't ambiguous. Tip: next time check some Maths textbooks or ask a Maths teacher

that one of the two shouldn’t even be a thing

Neither of them is a thing

not everybody shares your opinion and preferences

Facts you mean. The rules of Maths are facts

There is no mathematically true

There absolutely is! You just chose not to ask any experts about it

the most important thing with this “viral math” expressions is to recognize that

...they are all solvable by following the rules of Maths

One could argue that there should also be a strong connection between coefficients and variables (like in r=C/2π)

There is - The Distributive Law and Terms

it’s fine to stick to “BIDMAS” in school but be aware that that’s not the full story

No, BIDMAS and left to right is the full story

If you encounter such discussions in the wild you could just post a link to this page

No, post a link to this order of operations thread index - it has textbook references, proofs, memes, worked examples, the works!

FACT CHECK 4/5

a solidus (/) shall not be followed by a multiplication sign or a division sign on the same line

There's absolutely nothing wrong with doing that. The order of operations rules have everything covered. Anything which follows an operator is a separate term. Anything which has a fraction bar or brackets is a single term

most typical programming languages don’t allow omitting the multiplication operator

Because they don't come with order of operations built-in - the programmer has to implement it (which is why so many e-calculators are wrong)

“.NET IDE0048 – Add parentheses for clarity”

Microsoft has 3 different software packages which get order of operations wrong in 3 different ways, so I wouldn't be using them as an example! There are multiple rules of Maths they don't obey (like always rounding up 0.5)

Let’s say we want to clean up and simplify the following statement … o×s×c×(α+β) … by removing the explicit multiplication sign and order the factors alphabetically: cos(α+β) Nobody in their right mind would remove the explicit multiplication sign in this case

This is wrong in so many ways!

1. you did multiplication before brackets, which violates order of operations rules! You didn't give enough information to solve the brackets - i.e. you left it ambiguous - you can't just go "oh well, I'll just do multiplication then". No, if you can't solve Brackets then you can't solve ANYTHING - that is the whole point of the order of oeprations rules. You MUST do brackets FIRST.
2. the term (α+β) doesn't have a coefficient, so you can't just randomly decide to give it one. It is a separate term from the rest Is there supposed to be more to this question? Have you made this deliberately ambiguous for example?
3. if the question is just to simplify, then no simplification is possible. You've not given any values to substitute for the pronumerals
4. (α+β) is presumably (you've left this ambiguous by not defining them) a couple of angles, and if so, why isn't the brackets preceded by a trig function?
5. As it's written, it just looks like a straight-forward multiplying and adding pronumerals except you didn't give us any values for the pronumerals meaning no simplfication is possible
6. if this was meant to be a trig question (again, you've left out any information that would indicate this, making it ambiguous) then you wouldn't use c, o, or s for your pronumerals - you've got a whole alphabet left you can use. Appropriate choice of pronumerals is something we teach in Maths. e.g. C for cats, D for dogs. You haven't defined what ANY of these pronumerals are, leaving it ambiguous

Nobody will interpret cos(α+β) as a multiplication of four factors

7. as originally written it's 4 terms, not 1 term. i.e. it's not cos(α+β), it's actually oxsxxx(α+β), since that can't be simplified. And yes, that's 4 terms multiplied!

From those 7 points, we can see this is not a real Maths problem. You deliberately made it ambiguous (didn't say what any of the pronumerals are) so you could say "Look! Maths is ambiguous!". In other words, this is a strawman. If you really think Maths is ambiguous, then why didn't you use a real Maths example to show that? Spoiler alert: #MathsIsNeverAmbiguous hence why you don't have a real example to illustrate ambiguity

Implicit multiplications of variables with expressions in parentheses can easily be misinterpreted as functions

No they can't. See previous points. If there is a function, then you have to define what it is. e.g. f(x)=x². If no function has been defined, then f is the pronumeral f of the factorised term f(x), not a function. And also, if there was a function defined, you wouldn't use f as a pronumeral as well! You have the whole rest of the alphabet left to use. See my point about we teach appropriate choice of pronumerals

So, ambiguity really hides everywhere

No, it really doesn't. You just literally made up some examples which go against the rules of Maths then claimed "Look! Maths is ambiguous!". No, it isn't - the rules of Maths make sure it's never ambiguous

IMHO it would be smarter to only allow the calculation if the input is unambiguous.

Which is exactly what calculators do! If you type in something invalid (say you were missing a bracket), it would say "syntax error" or something similar

force the user to write explicit multiplications

Are you saying they shouldn't be allowed to enter factorised terms? If so, why?

force notation that is never ambiguous

We already do

but that would lead to a very convoluted mess that’s hard to read and write

In what way is 6/2(1+2) either convoluted or hard to read? It's a term divided by a factorised term - simple

providing context that makes it unambiguous

In other words, follow the rules of Maths.

Links about various potentially ambiguous math notations

Spoiler alert: they're not

“Most ambiguous phrases and notations in maths”

e.g. fx=f(x), which I already addressed. It's either been defined as a function or as pronumerals, therefore nothing ambiguous

“Absolute value notation is ambiguous”

No, it's not. |a|b|c| is the absolute value of a, times b, times the absolute value of c... which you would just write as b|ac|. Unlike brackets you can't have nested absolute values, so the absolute value of (a times the absolute value of b times c) would make no sense, especially since it's the EXACT same answer as |abc| anyway!

In-line power towers like

Left associativity. i.e. an exponent is associated with the term to its left - solve exponents right to left

People saying "I don't know how to interpret this" doesn't mean it's ambiguous, nor that it isn't defined. It just means, you know, they need to look it up (or ask a Maths teacher)! If someone says "I don't know what the word 'cat' means", you don't suddenly start running around saying "The word 'cat' is ambiguous! The word 'cat' is ambiguous!" - you just tell them to look it up in a dictionary. In the case of Maths, you look it up in a Maths textbook

Because the actual math is easy almost everybody has an opinion on it

...and any of them which contradict any of the rules of Maths are demonstrably wrong

Most people also don’t know that with weak and strong juxtaposition there are two conflicting conventions available

...and Maths teachers know that both of them are made-up and not real things in Maths

But those mnemonics cover just the basics. The actual real world is way more complicated and messier than “BODMAS”

Nope. The mnemonics plus left to right covers everything you need to know about it

Even people who know about implicit multiplication by juxtaposition dismiss a lot of details

...because it's not a real thing

Probably because of confirmation bias and/or because they don’t want to invest so much time into thinking about stupid social media posts

...or because they're a high school Maths teacher and know all the rules of Maths

the actual problem with the ambiguity can’t be explained in a quick comment

Yes it can...

Forgotten rules of Maths - The Distributive Law (e.g. a(b+c)=(ab+ac)) applies to all bracketed Terms, and Terms are separated by operators and joined by grouping symbols

Bam! Done! Explained in a quick comment

FACT CHECK 3/5

It’s only a matter of taste and how widespread a convention or notation is

The rules are in every high school Maths textbook. The notation for your country is in your country's Maths textbooks

There are no arguments or proofs about what definition is correct

1+1=2 by definition (or whatever the notation is in your country). If you write 1+1=3 then that is wrong by definition

I found a lot of explanations online that were either half-assed or just plain wrong

And you seem to have included most of them so far - "implicit multiplication", "weak juxtaposition", "conventions", etc.

You either were taught something wrong or you misremember it.

Spoiler alert: It's always the latter

IMHO the mnemonics would be better without “division” and “subtraction”, because it would force people to think about it before blindly applying something the wrong way – “PEMA” for example. Parentheses, exponentiation, multiplication, addition

In fact what would happen is now people wouldn't know in what order to do division and subtraction, having removed them from the mnemonic (and there's absolutely no reason at all to remove them - you can do everything in the mnemonic order and it works, provided you also obey the left-to-right rule, which is there to make sure you obey left associativity)

parenthesis and exponents students typically don’t learn the order of operations through some mnemonics they remember them through exercise

That's not true at all. Have you not read through some of these arguments? They're all full of "Use BEDMAS!", "Use PEMDAS!", "It's PEMDAS not BEDMAS!" - quite clearly these people DID learn order of operations through the mnemonics

trying to remember some random acronyms

There's no requirement to memorise any acronym - you can always just make up your own if you find that easier! I did that a lot in university to remember things during the exam

they also state to “not use × to express a simple product”

...because a product is a Term, and to insert a x would break it into 2 Terms

A product is the result of a multiplication

The center dot also should not be used to mean a simple product

Exact same reason. They are saying "don't turn 1 term into 2 terms". To put that into the words that you keep using, "don't use weak juxtaposition"

Nobody at the American Physical Society (at least I hope) would say that 6/2×3 equals one, because that’s just bonkers

Because it would break the rule of left associativity (i.e. left to right). No-one is advocating "multiplication before division" where it would violate left to right (usually by "multiplication" they're actually referring to Terms, and yes, you literally always have to do Terms before Division)

÷ (obelus), : (colon) or / (solidus), but that is not the case and they can be used interchangeably without any difference in meaning. There are no widespread conventions, that would attribute different meanings

Yes there is. Some countries use : for divide, whereas other countries use it for ratio

most standards forbid multiple divisions with inline notation, for example expressions like this 12/6/2

Name one! Give me a reference! There's nothing forbidding that in Maths (though we would more usually write it as 12/(6x2)). Again, all you have to do is obey left to right

Funny enough all the examples that N.J. Lennes list in his letter use

...Terms. Same as all textbooks do now

and thus his rule could be replaced by

...Terms, the already-existing rule that he apparently didn't know about (he mentions them, and products, but manages to completely miss what that actually means)

“Something, something, distributive property, something ….”

Something, something, Distributive Law (yes, some people use the wrong name, but in talking about the property, not the law, you're knocking down a strawman)

The distributive property is just a property that applies to some operations

...and The Distributive Law applies to every bracketed term that has a coefficient, in this case it's 2(1+2)

It has nothing to do with the order of operations

And The Distributive Law has everything to do with order of operations, since solving Brackets is literally the first step!

I’ve no idea where this idea comes from

Maybe you should've asked someone. Hint: textbooks/teachers

because there aren’t any primary sources (at least I wasn’t able to find any)

Here it is again, textbook references, proofs, memes, the works

should be calculated (distributed) first

Bingo! Distribution isn't Multiplication

6÷2(3). If we follow the strong juxtaposition convention, we must

...distribute the 2, always

It has nothing to do with the 3 being inside parentheses

It has everything to do with there being a coefficient to the brackets, the 2

Those parentheses are only there, because

...it's a factorised term, and the opposite of factorising is The Distributive Law

the parentheses do not force the multiplication

No, it forces distribution of the coefficient. a(b+c)=(ab+ac)

The parentheses are only there to make it clear that

...it is a factorised term subject to The Distributive Law

we are implicitly multiplying two separate numbers.

They're NOT 2 separate numbers. It's a single, factorised term, in the same way that 2a is a single term, and in this case a is equal to (1+2)!

With the context that the engineer is trying to calculate the radius of a circle it’s clear that they meant r=C/(2π)

Because 2π is a single term, by definition (it's the product of a multiplication), as is r itself, so that should actually be written r=(C/2π)

When symbols for quantities are combined in a product of two or more quantities, this combination is indicated in one of the following ways: ab,a b,a⋅b,a×b

Incorrect. Only the first one is a term/product (not separated by any operators) - the last 2 are multiplications, and the 2nd one is literally meaningless. Space isn't defined as meaning anything in Maths

Division of one quantity by another is indicated in one of the following ways:

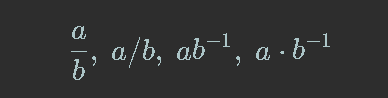
The first is a fraction

The second is a division

The third is also a fraction

The last is a multiplication by a fraction

Creates ambiguity since space isn't defined to mean anything in Maths. Looks like a typo - was there meant to be a multiply where the space is? Or was there not meant to be a space??

By definition ab^-1^=a^1^b^-1^=(a/b)

FACT CHECK 2/5

The behaviour is intended and even carefully documented in the manual

...and yet still a bug (I saw at least one other person point this out to you)

A few years ago, there was a Microsoft feature intended for people in China, but people who weren't in China were getting that behaviour. i.e. a bug. It was documented and a deliberate design choice for people in China, but if you weren't in China then it's a bug. Just documenting a design choice doesn't mean bugs don't happen. A calculator giving a wrong answer is a bug

weak juxtaposition is only used by old calculators

Based on the comments in the above video, the opposite is true - this problem first arose in '96

because they are scientific calculators.

So the person programming it is far more likely to need to check their Maths first - bingo!

TI (Texas Instruments) also has some calculators that use strong juxtaposition and some products that use weak juxtaposition

...and some that use both! i.e. some follow Terms but not The Distributive Law. As I said to begin with, these are 2 DIFFERENT rules, and you can't just lump them together as one

evaluate 1/2X as 1/(2X)

Which is correct, as per Terms

while other products may evaluate the same expression as 1/2X from left to right

What you mean is they evaluate it as 1/2xX, since 1/2X and 1/(2X) are the same thing

it would be necessary to group 2X in parentheses

No, not necessary, since 2a=(2xa) by definition, alluded to in Cajori in 1928...

Sharp is a bit of an exception here, because all their other scientific calculators seem to

...follow all the rules of Maths, always. There's something to be said for making sure you're doing it right. :-)

Google uses the same priority for explicit and implicit multiplication

...and they will actually remove brackets I have put in and replace them with their own ("hi" to all the people who say you can fix any calculator by "just add more brackets" - Google doesn't CARE what brackets you've added!)

Desmos and GeoGebra try to force the user into using fractions (which is a good design decision if you ask me)

It's not, because a ÷ isn't a fraction bar. They're joining 2 terms into one and thus sometimes changing the answer

A lot of other tools like programming languages, spreadsheets, etc. don’t allow implicit multiplication syntax at all

It's not that they don't allow it, it's that it's not provided with the language by default in the first place! Most languages only provide you with some numbers, operators, and a few functions (like round), and it's up to the programmer to implement the rest. Welcome to why there are so many wrong e-calculators

let you choose if you want weak or strong juxtaposition

...which is a red flag to not use that calculator!

This gives you more control about how you like the calculator to behave in these situations

I'm not sure it does. I'd have to switch on "strong juxtaposition" (the only kind there is) and see what else has been disobeyed in Maths. e.g. Google removing my brackets and adding different ones

Wolfram|Alpha only uses strong juxtaposition between named variables, but weak juxtaposition for everything else. This might seem strange and inconsistent at first but is probably the least surprising behaviour for most people

I find any exceptions to following the rules of Maths surprising! No, you can't just make up your own rules

many textbooks, “a/bc” is intended to denote a/(bc)

a/bc=a/(bc) in every textbook

Wolfram Language, it means (a/b)×c

Welcome to "we're gonna add brackets to what you typed in and change the answer"

a multiplication sign has been omitted

...then that means it's not "multiplication" - it's Terms and/or The Distributive Law. The "M" in the mnemonics refers literally to multiplication signs, nothing else

Multiplication and division have the same priority, they are “mathematically speaking” the same operation. This also applies to addition and subtraction. One is just the inverse function of the other

Yep, and The Distributive Law and Factorising are the inverse of each other

no rule about “multiplication before division” or “division before multiplication” they always have the same priority

...and Brackets is always first, so in this case it doesn't even matter

In no way do any of the mnemonics represent any standard or norm in mathematics

Yes they do - mnemonics represent the actual order of operations rules

most children don’t become mathematicians later in life and if they do, they will learn all the other important stuff about the order of operations later

No, they won't. Year 8 is the last time order of operations is taught, and they have been taught everything they need to know about it by then

it’s hard to pump so much knowledge into children and teenagers

...and yet have you not noticed that teenagers almost never get this wrong - only adults do

Using “PEMDAS” to argue about the order of operations in mathematics

...is a totally valid thing to do. The problem is people classifying Distribution (Brackets/Parentheses with a coefficient) as "Multiplication", when there's literally no multiplication sign

Math notations and conventions evolve exactly like natural languages

No they don't. Maths is universal

A lot of it is heavily based on historical thanks and work from previous generations

It's all based on definitions and proofs, which are immutable

There is no definitive norm, standard or convention of notations and order of operations

You can find them in any high school textbook in your country (notation varies by country, but the rules don't)

some words only appear in half of them (like “implicit multiplication by juxtaposition”)

"implicit multiplication" doesn't appear in any Maths textbooks

sentences like “I saw the man with the telescope”, because it’s not clear if you saw him through the telescope or saw him holding (or looking through) a telescope

Yes it is clear (as I think I saw someone already point out here)

I saw the man with the telescope - the man has the telescope

I saw the man, with the telescope - I saw the man through a telescope

I saw the man through the telescope - I saw the man through a telescope

it should also be clear why there are no arguments or proofs for any side

But there are proofs! (There you go again with the "there is no..." red flag) Order of operations proof

FACT CHECK 1/5

If you are sure the answer is one... you are wrong

No, you are. You've ignored multiple rules of Maths, as we'll see...

it’s (intentionally!) written in an ambiguous way

Except it's not ambiguous at all

There are quite a few people who are certain(!) that their result is the only correct answer

...and an entire subset of those people are high school Maths teachers!

What kind of evidence/information would it take to convince you, that you are wrong

A change to the rules of Maths that's not in any textbooks yet, and somehow no teachers have been told about it yet either

If there is nothing that would change your mind, then I’m sorry I can’t do anything for you.

I can do something for you though - fact-check your blog

things that contradict your current beliefs.

There's no "belief" when it comes to rules of Maths - they are facts (some by definition, some by proof)

How can math be ambiguous?

#MathsIsNeverAmbiguous

operator priority with “implied multiplication by juxtaposition”

There's no such thing as "implicit multiplication". You won't find that term used anywhere in any Maths textbook. People who use that term are usually referring to Terms, The Distributive Law, or most commonly both! #DontForgetDistribution

This is a valid notation for a multiplication

Nope. It's a valid notation for a factorised Term. e.g. 2a+2b=2(a+b). And the reverse process to factorising is The Distributive Law. i.e. 2(a+b)=(2a+2b).

but the order of operations it’s not well defined with respect to regular explicit multiplication

The only type of multiplication there is is explicit. Neither Terms nor The Distributive Law is classed as "multiplication"

There is no single clear norm or convention

There is a single, standard, order of operations rules

Also, see my thread about people who say there is no evidence/proof/convention - it almost always ends up there actually is, but they didn't look (or didn't want you to look)

The reason why so many people disagree is that

...they have forgotten about Terms and/or The Distributive Law, and are trying to treat a Term as though it's a "multiplication", and it's not. More soon

conflicting conventions about the order of operations for implied multiplication

Let me paraphrase - people disagree about made-up rule

Weak juxtaposition

There's no such thing - there's either juxtaposition or not, and if there is it's either Terms or The Distributive Law

construct “viral math problems” by writing a single-line expression (without a fraction) with a division first and a

...factorised term after that

Note how none of them use a regular multiplication sign, but implicit multiplication to trigger the ambiguity.

There's no ambiguity...

multiplication sign - multiplication

brackets with no multiplication sign (i.e. a coefficient) - The Distributive Law

no multiplication sign and no brackets - Terms (also called products by some. e.g. Lennes)

If it’s a school test, ask you teacher

Why didn't you ask a teacher before writing your blog? Maths tests are only ever ambiguous if there's been a typo. If there's no typo's then there's a right answer and wrong answers. If you think the question is ambiguous then you've not studied enough

maybe they can write it as a fraction to make it clear what they meant

This question already is clear. It's division, NOT a fraction. They are NOT the same thing! Terms are separated by operators and joined by grouping symbols. 1÷2 is 2 terms, ½ is 1 term

BTW here is what happened when someone asked a German Maths teacher

you should probably stick to the weak juxtaposition convention

You should literally NEVER use "weak juxtaposition" - it contravenes the rules of Maths (Terms and The Distributive Law)

strong juxtaposition is pretty common in academic circles

...and high school, where it's first taught

(6/2)(1+2)=9

If that was what was meant then that's what would've been written - the 6 and 2 have been joined together to make a single term, and elevated to the precedence of Brackets rather than Division

written in an ambiguous way without telling you what they meant or which convention to follow

You should know, without being told, to follow the rules of Maths when solving it. Voila! No ambiguity

to stir up drama

It stirs up drama because many adults have forgotten the rules of Maths (you'll find students get this right, because they still remember)

Calculators are actually one of the reasons why this problem even exists in the first place

No, you just put the cart before the horse - the problem existing in the first place (programmers not brushing up on their Maths first) is why some calculators do it wrong

“line-based” text, it led to the development of various in-line notations

Yes, we use / to mean divide with computers (since there is no ÷ on the keyboard), which you therefore need to put into brackets if it's a fraction (since there's no fraction bar on the keyboard either)

With most in-line notations there are some situations with conflicting conventions

Nope. See previous comment.

different manufacturers use different conventions

Because programmers didn't check their Maths first, some calculators give wrong answers

More often than not even the same manufacturer uses different conventions

According to this video mostly not these days (based on her comments, there's only Texas Instruments which isn't obeying both Terms and The Distributive Law, which she refers to as "PEJMDAS" - she didn't have a manual for the HP calcs). i.e. some manufacturers who were doing it wrong have switched back to doing it correctly

P.S. she makes the same mistake as you, and suggests showing her video to teachers instead of just asking a teacher in the first place herself (she's suggesting to add something to teaching which we already do teach. i.e. ab=(axb)).

none of those two calculators is “wrong”

ANY calculator which doesn't obey all the rules of Maths is wrong!

Bugs are – by definition – unintended behaviour. That is not the case here

So a calculator, which has a specific purpose of solving Maths expressions, giving a wrong answer to a Maths expression isn't "unintended behaviour"? Do go on

That you’re still wrong?

About? You haven't pointed out anything that's wrong.

the problem is written poorly due to the obelus and thus is open to interpretation

Oh, you're one of those people. Good, maybe we can finally get an answer then (this was also talked about in the blog). What other interpretation of an obelus is possible other than division? People keep saying it's ambiguous, but no-one has ever said why (other than some stuff that makes no sense in the context, as explained in the blog)

The distributive property is sometimes called the distributive law of multiplication and division

Yes, and sometimes people call Koalas "Koala bears", but that doesn't mean they're bears. Now bearing that in mind, read again what Khan said - the page which is called "Distributive property explained", not "Distributive Law explained".

Wait till you hear that “i before e except after c” wasn’t true either

Wait till you hear that's not a rule of Maths.

It’s wild that you think 7th grade math overrules grad school math though

Umm, never said anything of the kind...